(相加平均)≧(相乗平均)≧(調和平均)

定理

正の数 $a_1, a_2, \ldots, a_n$ の相加平均 $M$ , 相乗平均 $G$ , 調和平均 $H$ を次のように定義する.

$\displaystyle M = \frac{1}{n}\sum_{k=1}^n a_k$

$\displaystyle G = \sqrt[n]{\prod_{k=1}^n a_k}$

$\displaystyle H = \frac{n}{\sum_{k=1}^n \frac{1}{a_k}}$

このとき, 次の不等式が成り立つ.

$\displaystyle M\geqq G\geqq H$

等号成立は $a_1=a_2=\cdots=a_n$ のときのみ.

ただし, $\displaystyle \prod_{k=1}^n a_k=a_1\cdot a_2\cdots a_n$ (積を表す)とする.

この不等式を証明する問題は2005年の徳島大学入試で誘導無しで出ています.

←実際は誘導付きの問題として出題されていました. その問題と証明についてはこちら.

$n=2$ の場合については簡単に証明できるので, 高校でも習いますが, $n$ が 3 以上の証明は複雑になります.

証明

この不等式の証明方法はたくさんありますが, ここでは次の2通りを紹介します.

対数関数を用いる方法.
$n$ が2の累乗で表される場合を帰納的に示して, それ結果を利用してそれ以外の場合を示す方法.

1. の方法はシンプルですが, この方法は簡単には思いつけないでしょう.

2. の方法は少しややこしいですが, こちらの証明の方が自然な感じがします.

証明Ⅰ. 対数関数を用いる方法

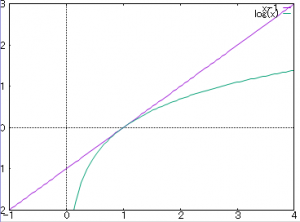
まず, 上のグラフからも分かるように, 正の $x$ に対して

(i): $\log{x}\leqq x-1$

が成り立つ. 等号は $x=1$ で成立する.

(グラフは縦が $y$ 軸, 横が $x$ 軸で, ピンクの線が $y=x-1$ , 緑が $y=\log{x}$ .)

相加平均と相乗平均の定義からM, Gは正であって, $\displaystyle\frac{a_k}{M} (k=1, 2, \ldots, n)$ は正. よって, 不等式(i)の $x$ の部分にこれを代入して,

$\displaystyle\log{\frac{a_k}{M}}\leqq \frac{a_k}{M}-1$

$k=1, 2, \ldots, n$ について和をとって,

$\displaystyle\sum_{k=1}^n \log{\frac{a_k}{M}}\leqq\sum_{k=1}^n\left(\frac{a_k}{M}-1\right)$

和の部分を計算すると

$\displaystyle\log{\frac{a_1a_2\ldots a_n}{M^n}}\leqq \frac{a_1+a_2+\cdots+a_n}{M}-n$

相加平均と相乗平均の定義を用いて

$\displaystyle\log{\frac{G^n}{M^n}}\leqq\frac{nM}{M}-n$

$\displaystyle n\log{\frac{G}{M}}\leqq 0$

よって, $\displaystyle\log{\frac{G}{M}}\leqq 0$ より $\displaystyle\frac{G}{M}\leqq 1$

$\therefore M \geqq G$ .

等号成立は $\displaystyle \frac{a_1}{M}=\frac{a_2}{M}=\cdots=\frac{a_n}{M}$ より $a_1=a_2=\cdots=a_n$ のとき.

また, 相乗平均と調和平均の間の不等号については, $\displaystyle\frac{1}{a_1}, \frac{1}{a_2}, \ldots, \frac{1}{a_n}$ について(相加平均)≧(相乗平均)を考えることで導かれます.

証明Ⅱ. nが2の累乗で表される場合を帰納的に示して, それ結果を利用してそれ以外の場合を示す方法.

この証明は1. の証明に比べてややこしく, 長くなります. $n\geqq 2$ の場合の $M\geqq G$ のみ示します.

(i) : $n=2^i$ と表せるとき ( $i$ は自然数)

[1] : $n=2^1=2$ のとき

$\displaystyle\left\{\frac{a_1+a_2}{2}\right\}^2-(\sqrt{a_1a_2})^2=\frac{1}{4}(a_1-a_2)^2\geqq 0$

より, $\displaystyle\frac{a_1+a_2}{2}\geqq\sqrt{a_1a_2}$ .

[2] : $n=2^i$ のとき成り立つと仮定する.

仮定: $\displaystyle \frac{1}{2^i}\sum_{k=1}^{2^i} a_k\geqq\left(\prod_{k=1}^{2^i}a_k\right)^{\frac{1}{2^i}}$

$n=2^{i+1}$ のときを考えると,
\begin{align}
\frac{1}{2^{i+1}}\sum_{k=1}^{2^{i+1}}a_k &= \displaystyle\frac{1}{2}\left(\frac{1}{2^i}\sum_{k=1}^{2^i} a_k+\frac{1}{2^i}\sum_{k=1}^{2^i}a_{k+2^i}\right) \\
&\geqq \left\{\left(\frac{1}{2^i}\sum_{k=1}^{2^i}a_k\right)\left(\frac{1}{2^i}\sum_{k=1}^{2^i}a_{k+2^i}\right)\right\}^{\frac{1}{2}}\\
&\geqq \left\{\left(\prod_{k=1}^{2^i}a_k\right)^{\frac{1}{2^i}}\left(\prod_{k=1}^{2^i}a_{k+2^i}\right)^{\frac{1}{2^i}}\right\}^{\frac{1}{2}} \\
&= \left(\prod_{k=1}^{2^{i+1}}a_k\right)^{\frac{1}{2^{i+1}}}
\end{align}
となり不等式が成立.

(ii) : $n=2^i$ と表せないとき

$2^{i-1}< n<2^i$ となる $i$ に対して, 新しく数 $a_{n+1}=a_{n+2}=\cdots=a_{2^i}=M$ を導入します.

(i)の結果から,

$\displaystyle\frac{1}{2^i}\sum_{k=1}^{2^i}a_k\geqq\left(\prod_{k=1}^{2^i}a_k\right)^{\frac{1}{2^i}}$

$\displaystyle\frac{1}{2^i}\left\{\left(\sum_{k=1}^n a_k\right)+\left(\sum_{k=n+1}^{2^i}M\right)\right\}\geqq\left\{\left(\prod_{k=1}^n a_k\right)\left(\prod_{k=n+1}^{2^i}M\right)\right\}^{\frac{1}{2^i}}$