数学の力

京大生が数学の定理・公式の証明や入試問題の解説をするブログ.

京大2013年度第1問を相似だけで解く

入試問題

スポンサードリンク

問題.

平行四辺形 $ABCD$ において, 辺 $AB$ を $1:1$ に内分する点を $E$ , 辺 $BC$ を $2:1$ に内分する点を $F$ 、辺 $CD$ を $3:1$ に内分する点を $G$ とする. 線分 $CE$ と線分 $FG$ の交点を $P$ とし, 線分 $AP$ を延長した直線と辺 $BC$ の交点を $Q$ とするとき, 比 $AP:PQ$ を求めよ.

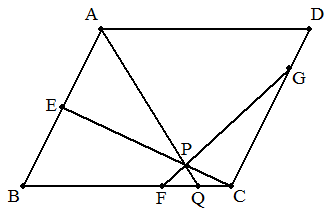
以前別の記事で, この問題をベクトルを使って解く方法を紹介しました. (--> こちら)

今回は, 同じ問題を三角形の相似を使って解きたいと思います.

解答.

まず, 三角形の相似を使うために補助線を引いておきます.

$CE$ を延長して直線 $AD$ と交わる点を $R$ ,

$FG$ を延長して直線 $AD$ と交わる点を $S$ とおきます.

また, 説明が分かりやすくなるように, 辺 $BC$ の長さを $x$ とおいておきます.

はじめに, $\triangle{PAR}$ と $\triangle{PQC}$ が相似なので, 求めるべき比 $AP:PQ$ は,

\begin{align*}
AP:PQ = RP:PC
\end{align*}

となります. さらに, $\triangle{PRS}$ と $\triangle{PCF}$ の相似に着目すると,

\begin{align*}
RP:CP = RS : CF
\end{align*}

となるので, $RS:CF$ の比を求めればいいことが分かります.

ここからはとても簡単です.

$BF:FC=2:1$ から,

\begin{align*}
CF=\dfrac{x}{3}
\end{align*}

はすぐに求まります.

$RS$ の長さは, $RA + AD + DS$ として考えます.

$RA$ は, $\triangle{RAE}$ と $\triangle{CBE}$ が相似で, 相似比は $AE:EB = 1:1$ なので,

\begin{align*}
RA = CB = x
\end{align*}

次に, $AD$ は, 平行四辺形の対辺の長さは等しいので, $BC$ に等しく

\begin{align*}
AD = x
\end{align*}

最後に, $DS$ は $\triangle{DSG}$ と $\triangle{CFG}$ が相似で, その相似比は $DG:CG = 1:3$ なので,

\begin{align*}
DS = \dfrac{1}{3}{CF} = \dfrac{x}{9}
\end{align*}

これらを足すと.

\begin{align*}
RS &= RA + AD + DS\\
&= x + x + \dfrac{x}{9}\\
&= \dfrac{19}{9}x
\end{align*}

したがって, 比は

\begin{align*}
RS : CF &= \dfrac{19}{9}x : \dfrac{x}{3}\\
&= 19:3
\end{align*}

なので, 答えは $AP : PQ = 19 : 3$ となります.

どの三角形の相似を使うのかをいちいち書く手間はありますが, 考え方や計算はベクトルで解くよりも簡単でした.