京大2021年度理系第5問(軌跡)

問題．

ーーー→　2021年度京大理系の他の問題はこちらから
第1問        第2問       第3問       第4問       第5問       第6問

第5問.
平面において，2点 に対し，点 は次の条件 を満たすとする．
  かつ点 の 座標は正．
次の各問に答えよ．
(1) の外心の座標を求めよ．
(2) 点 が条件 を満たしながら動くとき， の垂心の軌跡を求めよ．

(1) はいくつか考え方があるとは思いますが，この記事では余弦定理を使ってみます．

(2) の垂心については，①ベクトルで考える　②垂線の方程式から交点を求める　などの方法が考えられますが，今回は①の方法で解きます．

ちなみに，実際の入試で使うべきかは分かりませんが，オイラー線の性質(三角形の重心は，外心と垂心を結んだ線分を に内分する点) を使うと垂心は楽に求まります．

解答例．

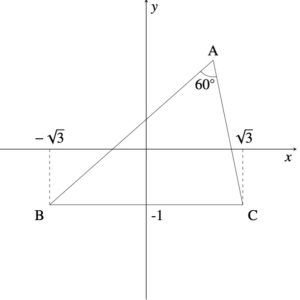
(1) 辺 の長さは なので， の外
接円の半径を とおいて余弦定理を使うと

\begin{align*}
2R &= \frac{2\sqrt{3}}{\sin60^\circ}\\
&= \frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}}\\
&= 4\\
\therefore R &= 2
\end{align*}

外心は辺 の垂直二等分線，つまり 軸上にあるので，その座標を とおくと，点 からの距離が なので

\begin{align*}
\{0-(-\sqrt{3})\}^2 + \{\alpha - (-1)\}^2 &= 2^2\\
(\alpha+1)^2 &= 1\\
\alpha+1 &= \pm 1\\
\therefore \alpha &= -2, 0
\end{align*}

となります．点 の 座標が正で なので，外心の 座標は でなければならないので，外心の座標は .

(2) (1) の結果から，点 は原点 を中心として半径 の円周の の部分を動くことがわかります．そこで，点 の座標を とおきます．

辺 は 軸に平行なので， から に下ろした垂線の方程式は . よって， の垂心の 座標は .

次に，垂心の 座標を とおくと，

また，

なので，

\begin{align*}
\overrightarrow{BH}\cdot\overrightarrow{AC} &= (2\cos\theta+\sqrt{3})(-2\cos\theta+\sqrt{3})+(t+1)(-2\sin\theta-1)\\
&= -4\cos^2\theta+3-2\sin\theta-1-(2\sin\theta+1)t\\
&= -4(1-\sin^2\theta)-2\sin\theta+2-(2\sin\theta+1)t\\
&= 4\sin^2\theta-2\sin\theta-2-(2\sin\theta+1)t\\
&= (2\sin\theta+1)(2\sin\theta-2)-(2\sin\theta+1)t\\
&= (2\sin\theta+1)(-t+2\sin\theta-2)
\end{align*}

より なので，.

※ 三角形の外心 ，重心 ，垂心 が を満たすことを用いると，外心が , 重心は から垂心 がすぐに求まります．

したがって，垂心の座標 は なので，

\begin{align*}
s^2 + (t+2)^2 &= 4\cos^2\theta + 4\sin^2\theta\\
&= 4
\end{align*}

より [tex: -2-2].

以上より， の垂心の軌跡は円 の の部分．

京大2021年度理系第4問(曲線の長さ)

問題．

ーーー→　2021年度京大理系の他の問題はこちらから
第1問        第2問       第3問       第4問       第5問       第6問

第4問.
曲線 の の部分の長さを求めよ．

問題自体はシンプルですね．公式に当てはめて，あとは積分がきちんと計算できるかどうかという問題です．

曲線の長さを求めるには以下の公式を使います．

曲線の長さを求める公式．
媒介変数 を用いて と表される曲線において， の部分の長さ は，
\begin{align*}
L &= \int_{t_0}^{t_1} \sqrt{\{f^\prime(t)\}^2+\{g^\prime(t)\}^2}\,\mathrm{d}t
\end{align*}特に，曲線 の の部分の長さ は
\begin{align*}
L &= \int_{x_0}^{x_1}\sqrt{\{1+f^\prime(x)\}^2}\,\mathrm{d}x
\end{align*}で表される．

解答例．

求める長さを とおくと，
\begin{align*}
L &= \int_0^{\frac{\pi}{2}} \sqrt{1+\left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)^2}\,\mathrm{d}x
\end{align*}

より，.

\begin{align*}
\sqrt{1+\left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)^2} &= \sqrt{1+\frac{\sin^2{x}}{(1+\cos{x})^2}}\\
&= \sqrt{\frac{(1+2\cos{x}+\cos^2{x})+\sin^2{x}}{(1+\cos{x})^2}}\\
&= \sqrt{\frac{2(1+\cos{x})}{(1+\cos{x})^2}}\\
&= \sqrt{\frac{2}{1+\cos{x}}}\\
&= \sqrt{\frac{1}{\cos^2{\frac{x}{2}}}}\\
&= \frac{1}{\cos{\frac{x}{2}}}\quad (\because 0\leqq x\leqq\frac{\pi}{2}より\cos\frac{x}{2}\geqq 0)
\end{align*}

よって，

\begin{align*}
L = \int_0^{\frac{\pi}{2}} \frac{1}{\cos{\frac{x}{2}}}\,\mathrm{d}x
\end{align*}

となります．後はこの積分を頑張って計算していきましょう．分母・分子に をかけて

\begin{align*}
L &= \int_0^{\frac{\pi}{2}} \frac{\cos\frac{x}{2}}{\cos^2\frac{x}{2}}\,\mathrm{d}x\\
&= \int_0^{\frac{\pi}{2}} \frac{\cos\frac{x}{2}}{1-\sin^2\frac{x}{2}}\,\mathrm{d}x
\end{align*}

とし，ここで とおくと， で， のとき , のとき なので，

\begin{align*}
L &= \int_0^{\frac{\sqrt{2}}{2}} \frac{2}{1-t^2}\,\mathrm{d}t\\
&= \int_0^{\frac{\sqrt{2}}{2}} \left(\frac{1}{1+t}+\frac{1}{1-t}\right)\,\mathrm{d}t\\
&= \Big[\log|1+t|-\log|1-t|\Big]_0^{\frac{\sqrt{2}}{2}}\\
&= \log\left(1+\frac{\sqrt{2}}{2}\right)-\log\left(1-\frac{\sqrt{2}}{2}\right)\\
&= \log\frac{2+\sqrt{2}}{2}-\log\frac{2-\sqrt{2}}{2}\\
&= \log\frac{2+\sqrt{2}}{2-\sqrt{2}}\\
&= \log\frac{\sqrt{2}+1}{\sqrt{2}-1}\\
&= \log(\sqrt{2}+1)^2\\
&= 2\log(\sqrt{2}+1).
\end{align*}

今回のような や の積分はたまに出題されるので，変数変換して計算する方法を覚えておくといいかと思います．