トレミーの定理(Ptoremy's theorem)
学校では教科書のコラムなどに出てくるだけの定理ですが, 知っているとセンター試験の図形の問題で楽ができることがあります. このページの下にある証明は, 上の定理の証明ですが, 実際には一般の四角形に関する次のような定理があります.
四角形 ABCD の辺の長さと対角線の長さについて以下の不等式が成り立つ.
ただし, 等号成立はこの四角形が円に内接するときのみ.
この定理の証明は別の記事に書きます.
証明.
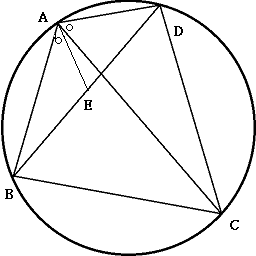
まず, となるような点 E を線分 BD 上にとります.
と
について,
\begin{align}
\angle{BAE}=\angle{CAD} \tag{1}
\end{align}
また, 円周角の定理より,
\begin{align}
\angle{ABE}=\angle{ACD} \tag{2}
\end{align}
(1), (2)より ∽
となり,
より
\begin{align}
AB\cdot CD&=AC\cdot BE \tag{3}
\end{align}
さらに, と
について,
また, 円周角の定理より
\begin{align}
\angle{ACB} = \angle{ADE} \tag{5}
\end{align}
(4), (5)より ∽
となり,
より
\begin{align}
AC\cdot ED=AD\cdot BC \tag{6}
\end{align}
よって, (3), (6)を用いると,
\begin{align}
AB\cdot CD+AD\cdot BC &= AC\cdot BE + AC\cdot ED\\
&= AC\cdot(BE+ED)\\
&= AC\cdot BD
\end{align}
