問題.
解答.
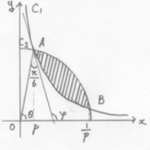
曲線 が直線
に関して対称であることから, 点 A と B も
に関して対称で,
.
直線 OA 及び A における の接線が
軸の正の方向となす角をそれぞれ
とおけば,
また, に対して
なので
.
与えられた条件から, で,
なので,
より,
. (2次方程式の解の公式により)
このことから,
\begin{align*}
\tan{\theta}&= \frac{1}{p^2}\\
&= \frac{1}{2-\sqrt{3}}\\
&= 2+\sqrt{3}
\end{align*}
\begin{align*}
\tan{2\theta} &= \frac{2(2+\sqrt{3})}{1-(2+\sqrt{3})^2}\\
&= -\frac{1}{\sqrt{3}}
\end{align*}
から
.
また, 円 の半径は
\begin{align*}
OA &= \sqrt{p^2+\frac{1}{p^2}}\\
&= \sqrt{(2-\sqrt{3})+(2+\sqrt{3})}\\
&= 2
\end{align*}
以上を踏まえて, 求める面積を とおくと,
\begin{align*}
S = \int_p^{\frac{1}{p}} \sqrt{4-x^2} dx - \int_p^{\frac{1}{p}} \frac{1}{x} dx
\end{align*}
右辺の第1項について, と置換して,
\begin{align*}
\int_p^{\frac{1}{p}} \sqrt{4-x^2} dx &= \int_{\theta}^{\frac{\pi}{2}-\theta} 2\sin{t}(-2\sin{t}) dt\\
&= -2\int_{\theta}^{\frac{\pi}{2}-\theta} (1-\cos{2t})dt\\
&= -2\Big[t-\frac{1}{2}\sin{2t}\Big]_\theta^{\frac{\pi}{2}-\theta} \\
&= \frac{2}{3}\pi
\end{align*}
右辺の第2項は
\begin{align*}
\int_p^{\frac{1}{p}} \frac{1}{x} dx &= \Big[\log|x|\Big]_p^{\frac{1}{p}}\\
&= \log{\frac{1}{p}}-\log{p}\\
&= \log{\frac{1}{p^2}}\\
&= \log{(2+\sqrt{3})}
\end{align*}
従って,
\begin{align*}
S=\frac{2}{3}\pi-\log{(2+\sqrt{3})}
\end{align*}
追記.
また, これは後に京大の教授から聞いた話ですが, 値を暗記していて からいきなり
と書くと減点対象だそうです. (つまり, 高校の範囲でその値を教えていないので導け, とのこと). そのため, ここでは2倍角の定理を使って
を求めています. ただ,同じ大学内でも学部によって採点基準が違ったりもするようなので,これは参考までに.