京大2014年度理系第3問(微分・最大値)

問題.

$\triangle{ABC}$ は, 条件 $\angle{B}=2\angle{A}$ , $BC=1$ を満たす三角形のうちで面積が最大のものであるとする. このとき, $\cos{\angle{B}}$ を求めよ.

微分して最大値を求める問題です. $\angle{B}$ の大きさはきれいな値として求まらないところと, 三角関数の変形(和と積の書き換え, 2倍角の公式など)を上手くできるかがポイントになってきます.

解答.

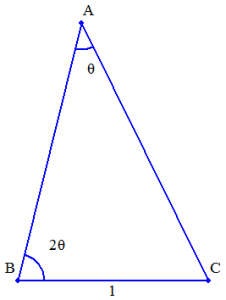
$\angle{A}=\theta$ とおくと, $\angle{B}=2\angle{A}=2\theta$ .

正弦定理より,

$\displaystyle \frac{AC}{\sin{\angle{B}}}=\frac{BC}{\sin{\angle{A}}}$ なので,

\begin{align*}
AC &= BC\cdot \frac{\sin{\angle{B}}}{\sin{\angle{A}}}\\
&= 1\cdot \frac{\sin{2\theta}}{\sin{\theta}}\\
&= \frac{2\sin{\theta}\cos{\theta}}{\sin{\theta}}\\
&= 2\cos{\theta}
\end{align*}

$\triangle{ABC}$ の面積を $S$ とすると,

\begin{align}
S &= \frac{1}{2}\cdot AC\cdot BC\sin{\angle{C}}\\
&= \frac{1}{2}\cdot 2\cos{\theta}\cdot 1\cdot \sin(\pi-3\theta)\\
&= \cos{\theta}\sin{3\theta}\\
&= \frac{1}{2}(\sin{4\theta}+\sin{2\theta}) \tag{1}
\end{align}

$S$ を $\theta$ で微分すると

\begin{align*}
\frac{dS}{d\theta} &= 2\cos{4\theta}+\cos{2\theta}\\
&= 2(2\cos^2{2\theta}-1)+\cos{2\theta}\\
&= 4\cos^2{2\theta}+\cos{2\theta}-2 \tag{2}
\end{align*}

三角形の内角の和が $\pi$ より, $0<3\theta<\pi$ なので, $\displaystyle 0<2\theta<\frac{2}{3}\pi$ で, $\displaystyle -\frac{1}{2}<\cos{2\theta}<1$ .

$\displaystyle \frac{dS}{d\theta}=0$ となるのは $\displaystyle \cos{2\theta}=\frac{-1+\sqrt{33}}{8}$ のときで, このときの $\theta$ の値を $\alpha$ とおくと, $S$ の増減表は下のようになり, $\theta=\alpha$ で $S$ は最大となります.