京大2013年度理系第1問文系第2問(ベクトル)

問題

平行四辺形 ABCD において, 辺 AB を 1:1 に内分する点を E, 辺 BC を 2:1 に内分する点を F、辺 CD を 3:1 に内分する点を G とする. 線分 CE と線分 FG の交点を P とし, 線分 AP を延長した直線と辺 BC の交点を Q とするとき, 比 AP:PQ を求めよ.

問題文にベクトルは出てこないですが, ベクトルを使って解く問題. 2直線の交点を求めるという定番の問題です.

実は, 線分を延長して三角形の相似を繰り返し使うことで, 初等幾何で答えを求めることもできますが…….(→京大2013年度第1問を相似だけで解く)

解答.

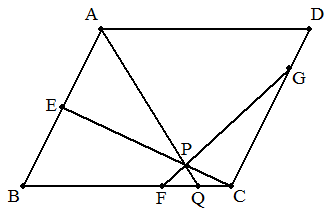
, とおくと,

\begin{align*}
\overrightarrow{AG}&= \overrightarrow{AD}+\overrightarrow{DG}\\
&= \frac{1}{4}\vec{b}+\vec{d}
\end{align*}

\begin{align*}
\overrightarrow{AF} &= \overrightarrow{AB}+\overrightarrow{BF}\\
&= \vec{b}+\frac{2}{3}\vec{d}
\end{align*}

点 P が線分 CE を に内分するとすると,

\begin{align}
\overrightarrow{AP} &= r\overrightarrow{AE}+(1-r)\overrightarrow{AC}\\
&= \frac{r}{2}\vec{b}+(1-r)(\vec{b}+\vec{d})\\
&= \left(1-\frac{r}{2}\right)\vec{b}+(1-r)\vec{d} \tag{1}
\end{align}

また, 点 P が線分 FG を に内分するとすると,

\begin{align}
\overrightarrow{AP} &= s\overrightarrow{AG}+(1-s)\overrightarrow{AF}\\
&= s\left(\frac{1}{4}\vec{b}+\vec{d}\right)+(1-s)\left(\vec{b}+\frac{2}{3}\vec{d}\right)\\
&= \left(1-\frac{3}{4}s\right)\vec{b}+\left(\frac{2}{3}+\frac{s}{3}\right)\vec{d} \tag{2}
\end{align}

と は1次独立なので, (1), (2)より,

\begin{align*}
\left\{\begin{array}{ll}
1-\frac{r}{2}=1-\frac{3}{4}s\\
1-r = \frac{2}{3}+\frac{s}{3}
\end{array}\right.
\end{align*}

これを解いて, .

よって, (5) より .

3点 A, P, Q は一直線上にあるので とおいて, を と で表すと,

\begin{align*}
\overrightarrow{AQ} &= k\left(\frac{19}{22}\vec{b}+\frac{8}{11}\vec{d}\right)\\
&= \frac{19}{22}k\vec{b}+\frac{8}{11}k(\overrightarrow{AC}-\vec{b})\\
&= \frac{3}{22}k\vec{b}+\frac{8}{11}k\overrightarrow{AC}
\end{align*}

点 Q は線分 BC 上にあるので, .

.

よって, .