数学の力

京大生が数学の定理・公式の証明や入試問題の解説をするブログ.

三角形の内角の2等分線を引いた長さに関する定理

定義・定理・公式

スポンサードリンク

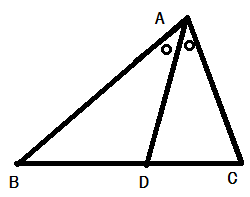
三角形の内角の2等分線を引いた長さに関する定理

定理.

定理 :

$\triangle{\mathrm{ABC}}$ の $\angle{\mathrm{A}}$ の2等分線と辺 $\mathrm{BC}$ の交点を $\mathrm{D}$ とすると,

${\mathrm{AD}}^2 = \mathrm{AB}\cdot \mathrm{AC} - \mathrm{BD}\cdot \mathrm{CD}$

が成り立つ.

この定理は三角形の角の2等分線に関する定理のページでも紹介しましたが, 中学や高校では習わない定理です. しかし知っておくと検算用としても便利です.

問題の例.

問 : $\mathrm{AB}=5$ , $\mathrm{AC}=3$ , $\mathrm{BC}=7$ である $\triangle{\mathrm{ABC}}$ について, $\angle{\mathrm{A}}$ の2等分線と辺 $\mathrm{BC}$ の交点を $\mathrm{D}$ とするとき, $\mathrm{BD}$ および $\mathrm{AD}$ の長さを求めよ.

答 :

角の2等分線の定理により,

$\mathrm{BD} : \mathrm{CD} = \mathrm{AB} : \mathrm{AC} = 5 : 3$

なので,

$\displaystyle \mathrm{BD} = 7\cdot \frac{5}{8}=\frac{35}{8}$

$\displaystyle \mathrm{CD} = 7\cdot \frac{3}{8} = \frac{21}{8}$

また, 上の定理より

$\displaystyle \mathrm{AD}^2 = 5\cdot 3 - \frac{35}{8}\cdot\frac{21}{8} = \frac{225}{64}$

となり,

$\displaystyle \mathrm{AD} = \frac{15}{8}$ .

証明.

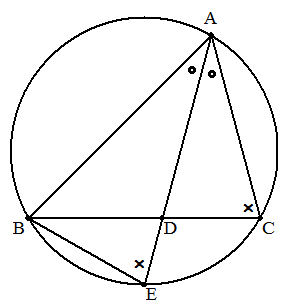
kakunonitoubunsen3

直線 $\mathrm{AD}$ と $\triangle{\mathrm{ABC}}$ の外接円との交点のうち $\mathrm{A}$ でない方の点を $\mathrm{E}$ とする.

弧 $\mathrm{AB}$ の円周角より,

$\angle{\mathrm{ACD}}=\angle{\mathrm{AEB}}$

また, 仮定より

$\angle{\mathrm{DAC}}=\angle{\mathrm{BAE}}$

なので,

$\triangle{\mathrm{ACD}}$ ∽ $\triangle{\mathrm{AEB}}$ .

よって,

$\mathrm{AD} : \mathrm{AB} = \mathrm{AC} : \mathrm{AE}$

より,

$\mathrm{AD}\cdot \mathrm{AE} = \mathrm{AB}\cdot \mathrm{AC}$

ところで, $\mathrm{AE}=\mathrm{AD}+\mathrm{DE}$ なので,

$\mathrm{AD}(\mathrm{AD}+\mathrm{DE})=\mathrm{AB}\cdot \mathrm{AC}$

$\therefore \mathrm{AD}^2=\mathrm{AB}\cdot \mathrm{AC} - \mathrm{AD}\cdot \mathrm{DE}$ .

方べきの定理を用いると,

$\mathrm{AD}\cdot \mathrm{DE} = \mathrm{BD}\cdot \mathrm{CD}$

が成り立つので,

$\mathrm{AD}^2 = \mathrm{AB}\cdot \mathrm{AC} - \mathrm{BD}\cdot \mathrm{CD}$

となる.