数学の力

京大生が数学の定理・公式の証明や入試問題の解説をするブログ.

三角形と角の2等分線に関する定理

定義・定理・公式

スポンサードリンク

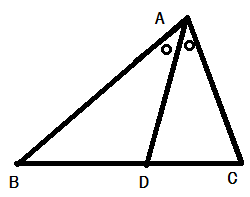
三角形と角の2等分線に関する定理

定理

定理1 :

$\triangle{\mathrm{ABC}}$ の $\angle{\mathrm{A}}$ の2等分線と辺 $\mathrm{BC}$ との交点を $\mathrm{D}$ とすると,

$\mathrm{AB} : \mathrm{AC} = \mathrm{BD} : \mathrm{DC}$

が成り立つ.

また, 三角形の外角の二等分線に関しても同様の定理が成り立ちます.

定理2 :

$\mathrm{AB}\neq \mathrm{AC}$ である $\triangle{\mathrm{ABC}}$ の $\angle{\mathrm{A}}$ の外角の2等分線と辺 $\mathrm{BC}$ の延長との交点を $\mathrm{D}$ とすると,

$\mathrm{AB} : \mathrm{AC} = \mathrm{BD} : \mathrm{DC}$

が成り立つ.

また, 次の定理は高校では習わないですが, 知っておくと検算用などで役に立ちます.

定理3 :

$\triangle{\mathrm{ABC}}$ の $\angle{\mathrm{A}}$ の2等分線と辺 $\mathrm{BC}$ の交点を $\mathrm{D}$ とすると,

${\mathrm{AD}}^2 = \mathrm{AB}\cdot \mathrm{AC} - \mathrm{BD}\cdot \mathrm{CD}$

が成り立つ.

三角形の3辺の長さが分かっていれば, 定理1を用いて $\mathrm{BD}$ , $\mathrm{CD}$ の長さが分かるので, この定理を用いれば $\mathrm{AD}$ の長さが簡単に求まります.

証明.

定理1.

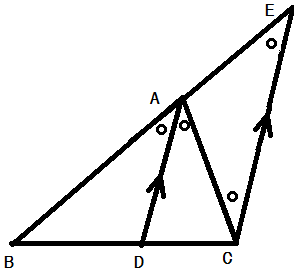
kakunonitoubunsen_prove1

点 $\mathrm{C}$ を通り $\mathrm{AD}$ に平行な直線を引いて, $\mathrm{BA}$ の延長との交点を $\mathrm{E}$ とすると,

同位角で $\angle{\mathrm{BAD}}=\angle{\mathrm{AEC}}$

錯角も等しく, $\angle{\mathrm{ACE}}=\angle{\mathrm{CAD}}$

仮定より $\angle{\mathrm{BAD}}=\angle{\mathrm{CAD}}$

でもあるから, $\angle{\mathrm{AEC}}=\angle{\mathrm{ACE}}$

となって, $\triangle{\mathrm{ACE}}$ は二等辺三角形で, $\mathrm{AC}=\mathrm{AE}$ .

一方で, $\triangle{\mathrm{BEC}}$ において $\mathrm{AD} /\!/ \mathrm{CE}$ より

$\mathrm{AB} : \mathrm{AE} = \mathrm{BD} : \mathrm{DC}$

よって, $\mathrm{AB} : \mathrm{AC} = \mathrm{BD} : \mathrm{DC}$ .

定理2.

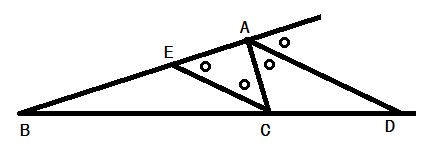
kakunonitoubunsen_prove2

点 $\mathrm{C}$ を通り, $\mathrm{AD}$ に平行な直線を引いて, $\mathrm{BA}$ との交点を $\mathrm{E}$ とすると, 定理1の場合同様に同位角, 錯角が等しいことを用いて,

$\angle{\mathrm{AEC}}=\angle{\mathrm{ACE}}$

となり, $\triangle{\mathrm{ACE}}$ は二等辺三角形で, $\mathrm{AC} = \mathrm{AE}$ .

一方で $\mathrm{AD} /\!/ \mathrm{CE}$ より

$\mathrm{AB} : \mathrm{AE} = \mathrm{BD} : \mathrm{CD}$

よって, $\mathrm{AB} : \mathrm{AC} = \mathrm{BD} : \mathrm{CD}$ .

定理3.

定理3の証明は別のページ(三角形の内角の2等分線を引いた長さに関する定理)を見てください.