四平方の定理 ~三平方の定理の拡張~

三平方の定理というと, 直角三角形において,

(斜辺の2乗) = (他の2辺の2乗の和)

が成り立つという有名な定理です.

ここでは, 三平方の定理(平面上の定理)を3次元に拡張した, 四平方の定理を紹介します.

定理.

3つの面が直角三角形で, 1つの頂点に直角が集まっている三角錐を考えるとき,

直角三角形の面の面積を $S_1, S_2, S_3$ , 残りのもう1つの面の面積を $S$ とすると,

\begin{align*}
S_1^2+S_2^2+S_3^2 = S^2
\end{align*}

が成り立つ.

下図のような, 直角をつくる3辺の長さがそれぞれ 1, 1, 2 の三角錐を考えます.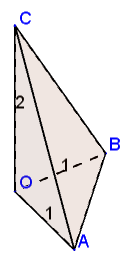

直角三角形の面の面積は,

$\begin{align} \triangle{OAB} &= \dfrac{1}{2}\\ \triangle{OBC} &= 1\\ \triangle{OCA} &= 1 \end{align}$

この三角錐の展開図は右のような正方形になり,

$\begin{align} \triangle{ABC} = 2\times 2 - \dfrac{1}{2}-1-1 = \dfrac{3}{2} \end{align}$

よって,

$\begin{align*} \left(\frac{1}{2}\right)^2+1^2+1^2 &= \frac{1}{4}+1+1\\ &= \frac{9}{4}\\ &= \left(\frac{3}{2}\right)^2 \end{align*}$

となり, 定理を満たしています.

数学の力