チェバの定理とその逆

チェバの定理

定理 : $\triangle{\mathrm{ABC}}$ の頂点 $\mathrm{A, B, C}$ と, この三角形の辺及びその延長上に無い点 $\mathrm{O}$ を結ぶ. 各直線が対辺またはその延長とそれぞれ点 $\mathrm{P}$ , $\mathrm{Q}$ , $\mathrm{R}$ で交わるとき, 次の等式が成り立つ.
$\displaystyle \frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}}=1$

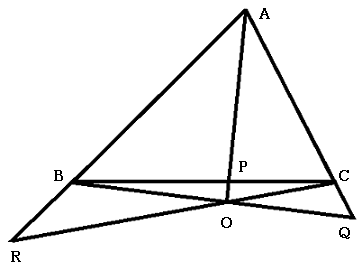
この定理では点 $\mathrm{O}$ が三角形の内部にある場合(左の図)と外側にある場合(右の図)があります. よく使うのは左の図の場合ですが, 右側のような場合も使えることを覚えておきましょう.

公式の覚え方としては, メネラウスの定理の場合とほとんど同じですが, 三角形の頂点と, 辺(またはその延長)上の点を交互にたどっていくイメージです.

チェバの定理の逆

定理：
$\triangle{\mathrm{ABC}}$ の辺 $\mathrm{BC}$ , $\mathrm{CA}$ , $\mathrm{AB}$ またはその延長上にそれぞれ点 $\mathrm{P}$ , $\mathrm{Q}$ , $\mathrm{R}$ があり, この3点のうち1個または3個が辺上の点であるとする. このとき,

$\mathrm{BQ}$ と $\mathrm{CR}$ が交わり, かつ

$\displaystyle \frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}}=1$

が成り立つならば, 3直線 $\mathrm{AP}$ , $\mathrm{BQ}$ , $\mathrm{CR}$ は1点で交わる.

証明

チェバの定理

点 $\mathrm{O}$ が $\triangle{\mathrm{ABC}}$ の内部にある場合, 外部にある場合にかかわらず,

三角形の面積と線分の比の関係から,

$\mathrm{BP}:\mathrm{PC}=\triangle{\mathrm{OAB}}:\triangle{\mathrm{OAC}}$

すなわち $\displaystyle \frac{\mathrm{BP}}{\mathrm{PC}}=\frac{\triangle{\mathrm{OAB}}}{\triangle{\mathrm{OAC}}}$

同様に,

$\displaystyle \frac{\mathrm{CQ}}{\mathrm{QA}}=\frac{\triangle{\mathrm{OBC}}}{\triangle{\mathrm{OAB}}}$

$\displaystyle \frac{\mathrm{AR}}{\mathrm{RB}}=\frac{\triangle{\mathrm{OAC}}}{\triangle{\mathrm{OBC}}}$

以上より,
$\begin{align*} \frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} &= \frac{\triangle{\mathrm{OAB}}}{\triangle{\mathrm{OAC}}}\cdot\frac{\triangle{\mathrm{OBC}}}{\triangle{\mathrm{OAB}}}\cdot\frac{\triangle{\mathrm{OAC}}}{\triangle{\mathrm{OBC}}}\\ &= 1 \end{align*}$