数学の力

京大生が数学の定理・公式の証明や入試問題の解説をするブログ.

メネラウスの定理とその逆

定義・定理・公式

スポンサードリンク

メネラウスの定理

定理 : $\triangle{\mathrm{ABC}}$ の辺 $\mathrm{BC}, \mathrm{CA}, \mathrm{AB}$ またはその延長が, 三角形の頂点を通らない直線 $\ell$ とそれぞれ点 $\mathrm{P, Q, R}$ で交わるとき, 次の等式が成り立つ. $\frac{\mathrm{BP}}{\mathrm{PC}}\cdot \frac{\mathrm{CQ}}{\mathrm{QA}}\cdot \frac{\mathrm{AR}}{\mathrm{RB}}=1$

Menelaus1

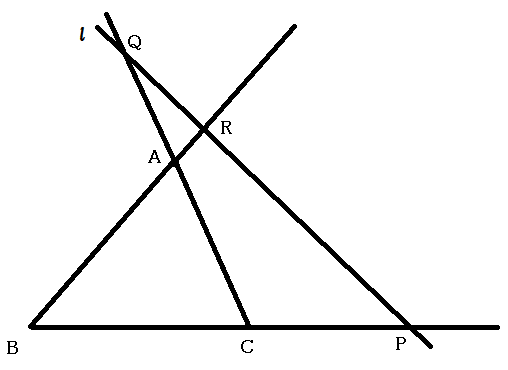Menelaus2

この定理では考えられる図として[1]の交点のうち 2 つが三角形の辺上にある場合と, [2]の 3 つの交点すべてが三角形の辺の延長上にある場合の 2 通りが考えられます.

[1]はよく使うのに対して, [2]の場合はたまにしか使わず, 気付きにくいですが, どちらも重要です.

この定理の式は見た目はややこしいですが, 三角形の頂点と, 直線 $\ell$ との交点とを交互にたどっていくイメージをすれば覚えやすいです.

(頂点 $B$ →交点 $P$ →頂点 $C$ →交点 $Q$ →頂点 $A$ →交点 $R$ →頂点 $B$ )

メネラウスの定理の逆

定理：
$\triangle{\mathrm{ABC}}$ の辺 $\mathrm{BC, CA, AB}$ またはその延長上に, それぞれ点 $\mathrm{P, Q, R}$ があり, この 3 点のうち 1 個または 3 個が辺の延長上の点であるとする. このとき,

$\displaystyle \frac{\mathrm{BP}}{\mathrm{PC}}\cdot \frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}}=1$

が成り立つならば, 3点 $\mathrm{P, Q, R}$ は一直線上にある.

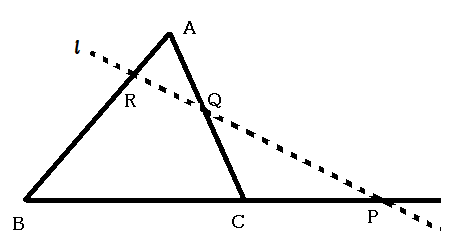
Menelaus_reverse1

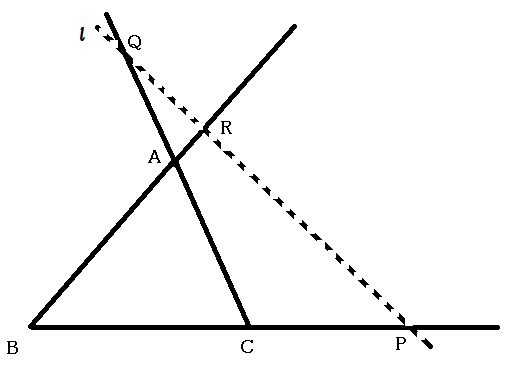Menelaus_reverse2

メネラウスの定理ほどではありませんが, こちらも重要な定理です.

証明

メネラウスの定理

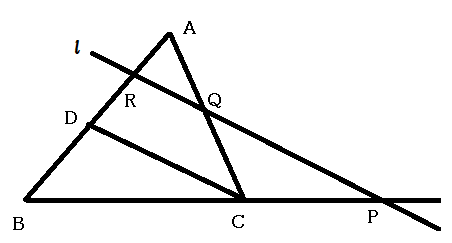
Menelaus_prove1

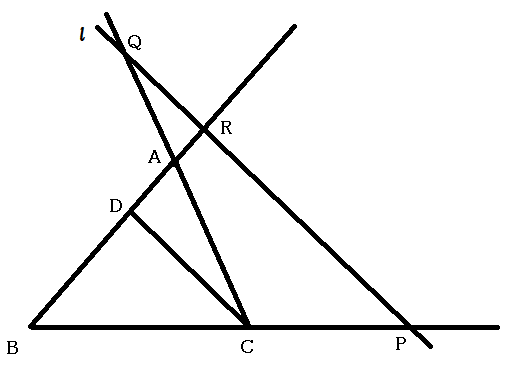
Menelaus_prove2

$\triangle{\mathrm{ABC}}$ の頂点 $\mathrm{C}$ を通り, 直線 $\ell$ に平行な直線を引き, 直線 $\mathrm{AB}$ との交点を $\mathrm{D}$ とすると, いずれの図の場合も平行線と比に関する定理から,

$\displaystyle \frac{\mathrm{BP}}{\mathrm{PC}}=\frac{\mathrm{BR}}{\mathrm{RD}}$

$\displaystyle\frac{\mathrm{CQ}}{\mathrm{QA}}=\frac{\mathrm{DR}}{\mathrm{RA}}$

よって,
$\begin{align} \frac{BP}{PC}\cdot \frac{CQ}{QA}\cdot \frac{AR}{RB} &= \frac{BR}{RD}\cdot\frac{DR}{RA}\cdot\frac{AR}{RB}\\ &= 1 \end{align}$

となる．　　　　▯

メネラウスの定理の逆

直線 $\mathrm{QR}$ と辺 $\mathrm{BC}$ の延長の交点を $\mathrm{P}^\prime$ とすると, メネラウスの定理より

$\displaystyle \frac{\mathrm{BP}^\prime}{\mathrm{P}^\prime \mathrm{C}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}}=1$

が成り立つが, 一方仮定より

$\displaystyle \frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}}=1$

なので,

$\displaystyle \frac{\mathrm{BP}^\prime}{\mathrm{P}^\prime \mathrm{C}}=\frac{\mathrm{BP}}{\mathrm{PC}}$

$\mathrm{P}$ と $\mathrm{P}^\prime$ はともに辺 $\mathrm{BC}$ の延長上にあるので, 2点 $\mathrm{P}$ と $\mathrm{P}^\prime$ は一致する.

よって, 3点 $\mathrm{P, Q, R}$ は一直線上にある. 　　　　▯

逆の証明にメネラウスの定理自身を使っているので不思議な感じですが, 元の定理とその逆は互いに独立の命題なので問題ありません.