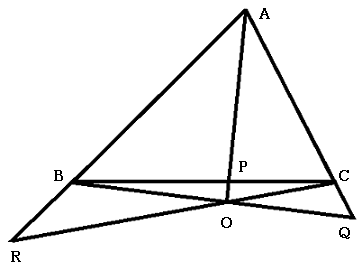
チェバの定理の逆
チェバの定理の逆は以下のようなものでした.と
が交わり, かつ
が成り立つならば, 3直線,
,
は1点で交わる.

今回は, この定理の利用例として, 三角形の重心, 内心, 垂心の存在証明をしてみます.
重心の存在
三角形の重心 :
三角形の3本の中線(頂点と向かい合った辺の中点を結ぶ線分)は1点で交わり, その点を重心という.
証明.
図のように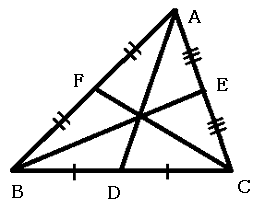
すると, 中線の定義から
\begin{align}
\mathrm{BD} &= \mathrm{CD}\\
\mathrm{CE} &= \mathrm{AE}\\
\mathrm{AF} &= \mathrm{BF}
\end{align}
なので,
\begin{align}
\frac{\mathrm{BD}}{\mathrm{DC}}\cdot \frac{\mathrm{CE}}{\mathrm{EA}}\cdot\frac{\mathrm{AF}}{\mathrm{FB}} &= 1\cdot 1\cdot 1\\
&= 1
\end{align}
となるので, チェバの定理の逆により3本の中線は1点で交わります.
内心の存在
三角形の内心 :
三角形の3つの内角の2等分線は1点で交わり, その交点を内心という.
証明.
図のように角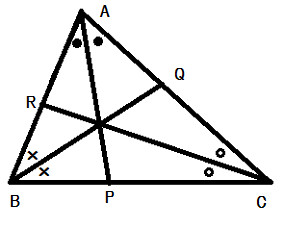
角の2等分線の定理により,
なので
同様に,
なので
なので
以上を辺々掛けて,
となるので, チェバの定理の逆により,
,
は1点で交わります.
垂心の存在
三角形の垂心 :
三角形の各頂点から対辺(またはその延長)に下ろした垂線は, 1点で交わり, その点を垂心という.
証明.
(ここでは鋭角三角形の場合を証明します. 直角三角形, 鈍角三角形の場合も同様にして証明できます. )の各頂点
,
,
から対辺に下ろした垂線の足をそれぞれ
,
,
とします.
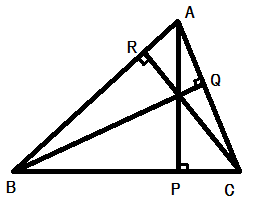
と
において,
が共通で,
より, 2組の角がそれぞれ等しく
∽
よって,
同様にして,
∽
より
∽
より
以上より,
となるので, チェバの定理の逆により,
,
は1点で交わります.